Definimos estas como:
Las curvas verticales son las que enlazan dos tangentes consecutivas de alineamiento vertical para que en su longitud se efectúe el paso gradual de la pendiente de la tangente de salida.
Pero...
¿Cuál es el objeto de estas?
El objeto de estas es que no existan cambio bruscos en la dirección vertical de los vehículos e movimiento en carreteras y ferrocarriles, generalmente la curva vertical es el arco de una parábola ya que esta se adapta bien al cambio gradual de dirección y permite el calculo rápido de las elevaciones sobre la curva.
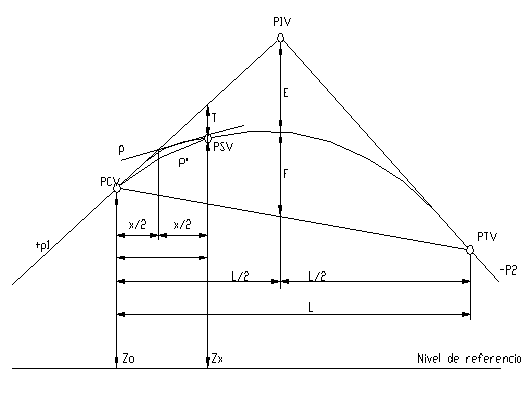
De esta manera se ve una curva vertical:
El diseño de las curvas verticales en cresta y en columpio es una función de la diferencia algebraica de las pendientes de las tangentes que se interceptan de la distancia de visibilidad de parada o de rebase, las cuales a su vez son función de la velocidad del proyecto de los vehículos y de la altura de la visión del conductor sobre la carretera y del drenaje. Además de estos factores, el diseño de las curvas verticales en columpio dependen también de las distancias que cubren el haz de luz de los faros de los vehículos de la comodidad del viajero y de la apariencia.
Para ampliar los criterios podemos mencionar los siguientes:
-Criterio de comodidad
-Criterio de apariencia
-Criterio de drenaje
-Criterio de seguridad
Para cada uno de los criterios existen formulas que regulan la LCV (Longitud de Curva Vertical). Estos criterios (y algotros agregados) corresponden a la ingeniería de carreteras, sin embargo en la topografía nos corresponde el trazo general de la rasante de la curva y nos interesaría también el criterio de drenaje y estableciendo el punto mas bajo de la curva, o mas alto.
Como topografía tomaremos una formula empírica bastante aproximada para la determinación mínima de longitud mínima de CV.
La formula es la siguiente:
LCV=0.6V ---------- Donde V es la velocidad del proyecto.
Por su Longitud las curvas pueden ser simétricas o asimétricas, estas tienen la siguiente forma:
CV Simétricas.
Si la distancia horizontal entre el PCV (Punto de comienzo vertical) y el PIV (Punto intermedio vertical) es igual a la distancia del PIV y el PTV (Punto de terminación vertical), se dice que la curva es simétrica.
CV Asimétricas.
.Cuando los lados de la curva vertical son desiguales, es decir el PCV hasta PIV es diferente del PIV hasta el PTV entonces es una Curva Vertical Asimétrica.
REPRESENTACION DE LAS DIFERENTES CURVAS VERTICALES.
Antes de esta representación, tenemos que mencionar la diferencia algebraica, que nos ayudara a identificar el tipo de CV que vamos a obtener dándole un simple vistazo a las pendientes de las tangentes que tenemos.
A = P1 - P2
Donde A es la diferencia de pendientes
P1 es la pendiente de entrada
P2 es la pendiente de salida
ELEMENTOS DE UNA CURVA VERRTICAL
PCV: Punto de comienzo vertical
PIV: Punto de intersección vertical
PTV: Punto de terminación vertical
e: External (es la mayor distancia entre la curva y el PIV)
ln: Longitud ya sea desde el PCV al PIV o del PTV al PIV
LCV: Longitud de Curva Vertical
P1: Pendiente de entrada
P2: Pendiente de salida
T (o bien Yn): Sera nuestra ordenada, o sea la distancia entre la curva y nuestra tangente
Xn: Distancia desde el PCV o el PTV hasta un estacionamiento.
Antes mencionamos como calculábamos la LCV en base a la velocidad de nuestro proyecto, ahora bien, ¿Cómo obtenemos los otros datos para iniciar nuestro proyecto?
Para nuestro numero de estacionamientos recurrimos a la siguiente ecuación:
Ne= (p1 - p2) / variación por estación
El porcentaje de cada estación es un valor que depende de la distancia de visibilidad necesaria para realizar un frenado; generalmente toma valores desde el 0.1% hasta el 1% dependiendo de la pendiente a usar.
External:
e =((P1-P2)/800) * LCV Esta ecuación es usada cuando nuestra CV es simétrica
e = ((L1*L2)/200LCV)*(P1-P2) Esta ecuación es usada cuando nuestra CV es asimétrica
Ordenada:
Yn = (Xn/Ln)^2 * e
PUNTO MAS BAJO/ALTO
¿Para que nos sirve saber la ubicación de este punto?
1) Para lo relacionado con los drenajes
2) Espacio libre de las estructuras de paso
3) Distancias de visibilidad
De toda esa información se necesita determinar su elevación y ubicación.
En los puntos de tangencia a la curva será horizontal y su pendiente por tanto será igual a cero.
Basándose en esta propiedad se usa la formula siguiente,
X= (P1*L)/(P1 - P2)
donde:
X= Distancia del PCV al punto mas bajo
P1= Pendiente de la tangente del PCV
P2= Pendiente de la tangente del PTV
L= Numero de estacionamientos
Pero esta formula cambia cuando nuestra curva es asimétrica, surgiendo dos ecuaciones para calcularla desde la izquierda o desde la derecha, las cuales son:
Xizq = (L1/L2)*((P1*L)/(P1 - P2))
donde L1 es la longitud desde el PCV al PIV y L2 es la longitud del PIV al PTV.
Xder = (L2/L1)*((P2*L)/(P1- P2))
PROCESO DE CALCULO
Para encontrar las elevaciones de los distintos puntos de la curva vertical se realiza el siguiente proceso.
1) Se divide la curva en tramos de distancias iguales.
2) se encuentran las elevaciones correspondientes a cada punto de la tangente
3) Calcular el valor de la ordenada o desviación en ese punto y restar o sumar este valor a la elevación de la tangente para obtener la elevación de cada punto de la curva
4) Posterior calcular el punto mas alto o bajo de la curva con su elevación y posición.
POSTERIOR A ESTE BLOG SE PRESENTARA UN EJEMPLO DE LA APLICACION DE ESTE PROCESO.